16. Доказать методом математической индукции, что для любого n∈N...
Приложения:
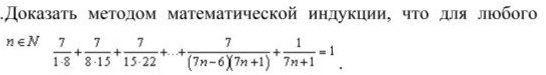
Ответы на вопрос
Ответил IrkaShevko
0
1) n = 1
верно, это база
2) предположим, что для n = k - верно
3) докажем, что для n = k+1 так же верно
![frac{7}{1*8} + frac{7}{8+15} +...+ frac{7}{(7k-6)(7k+1)}=1 - frac{1}{7k+1} \\
frac{7}{1*8} + frac{7}{8+15} +...+ frac{7}{(7k-6)(7k+1)}+ frac{7}{(7k+1)(7k+8)}+ frac{1}{7k+8} =\
=1- frac{1}{7k+1} + frac{7}{(7k+1)(7k+8)}+ frac{1}{7k+8} =1 - frac{7k+1-7k-8+7}{(7k+1)(7k+8)} =1](https://tex.z-dn.net/?f=+frac%7B7%7D%7B1%2A8%7D+%2B+frac%7B7%7D%7B8%2B15%7D+%2B...%2B+frac%7B7%7D%7B%287k-6%29%287k%2B1%29%7D%3D1+-++frac%7B1%7D%7B7k%2B1%7D+%5C%5C%0A+frac%7B7%7D%7B1%2A8%7D+%2B+frac%7B7%7D%7B8%2B15%7D+%2B...%2B+frac%7B7%7D%7B%287k-6%29%287k%2B1%29%7D%2B+frac%7B7%7D%7B%287k%2B1%29%287k%2B8%29%7D%2B+frac%7B1%7D%7B7k%2B8%7D+%3D%5C%0A%3D1-+frac%7B1%7D%7B7k%2B1%7D+%2B+frac%7B7%7D%7B%287k%2B1%29%287k%2B8%29%7D%2B+frac%7B1%7D%7B7k%2B8%7D+%3D1+-++frac%7B7k%2B1-7k-8%2B7%7D%7B%287k%2B1%29%287k%2B8%29%7D+%3D1 "frac{7}{1*8} + frac{7}{8+15} +...+ frac{7}{(7k-6)(7k+1)}=1 - frac{1}{7k+1} \\
frac{7}{1*8} + frac{7}{8+15} +...+ frac{7}{(7k-6)(7k+1)}+ frac{7}{(7k+1)(7k+8)}+ frac{1}{7k+8} =\
=1- frac{1}{7k+1} + frac{7}{(7k+1)(7k+8)}+ frac{1}{7k+8} =1 - frac{7k+1-7k-8+7}{(7k+1)(7k+8)} =1")
верно, по ММИ доказано
верно, это база
2) предположим, что для n = k - верно
3) докажем, что для n = k+1 так же верно
верно, по ММИ доказано
Новые вопросы