152 и 153
P.s Подробное решение
_._._._._._._._._._._._._._._
Приложения:

Ответы на вопрос
Ответил natalyabryukhova
1
Ответ:
45°
Объяснение:
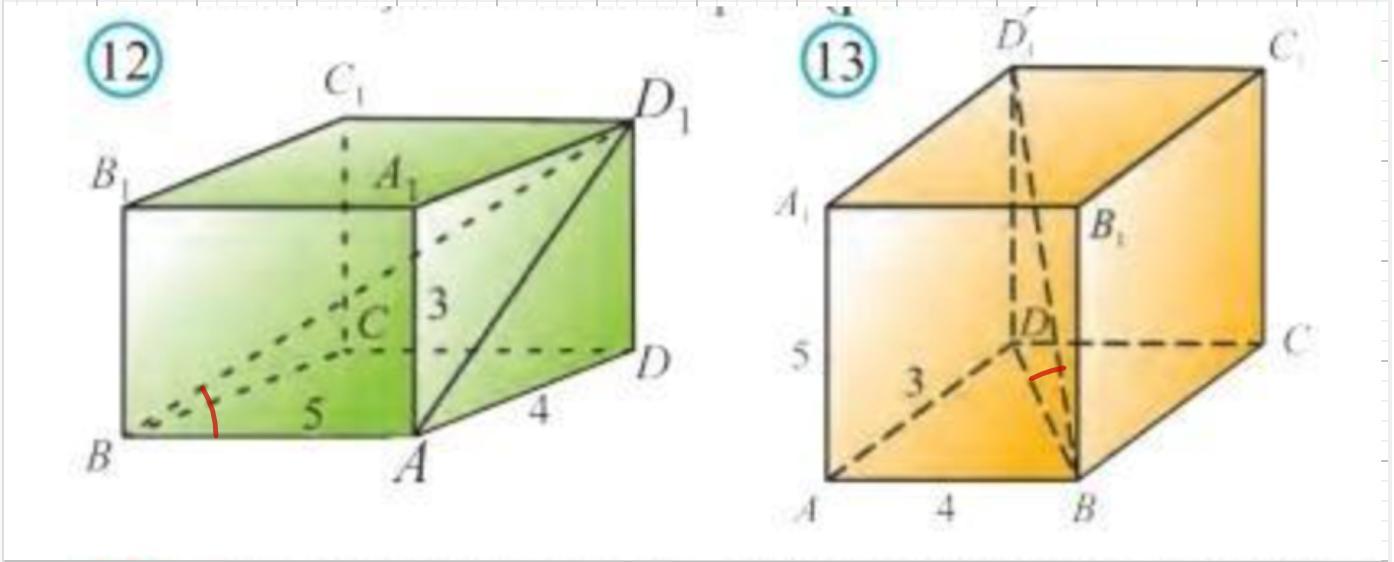
152. Дано: ABCDA₁B₁C₁D₁ - прямоугольный параллелепипед;
AB = 5; AD = 4; AA₁ = 3
Найти: ∠ABD₁.
Решение:
- Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
1. Рассмотрим ΔAA₁D₁ - прямоугольный.
- Противоположные сторона прямоугольника равны.
⇒ AD = A₁D₁
По теореме Пифагора:
2. Рассмотрим ΔABD₁.
AB ⊥ AD
- Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
⇒ ΔABD₁ = прямоугольный.
AB = BD₁= 5
⇒ ΔABD₁ - равнобедренный.
- Углы при основании равнобедренного треугольника равны.
⇒ ∠BD₁A = ∠ABD₁
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠BD₁A = ∠ABD₁ = 90°:2 = 45°
153. Дано: ABCDA₁B₁C₁D₁ - прямоугольный параллелепипед;
АВ = 4; AD = 3; AA₁ = 5.
Найти: ∠DBD₁
Решение:
Рассмотрим ΔADB - прямоугольный.
По теореме Пифагора:
Рассмотрим ΔDD₁B - прямоугольный.
AA₁ = DD₁ = 5 (противоположные стороны прямоугольника AA₁D₁D)
BD = DD₁=5
⇒ ΔDD₁B - равнобедренный.
- Углы при основании равнобедренного треугольника равны.
⇒ ∠DBD₁ = ∠DD₁B
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠DBD₁ = ∠DD₁B = 90° :2 = 45°
Приложения:
villiwonkka1:
Лучший ответ !
Новые вопросы
Українська мова,
1 год назад
Русский язык,
1 год назад
Математика,
6 лет назад
Другие предметы,
6 лет назад
Информатика,
8 лет назад