150 БАЛЛОВ ПОМОГИТЕ СРОЧНО ПЖ Упростите выражение и найдите его значение
(y+7)2 + 2(y +7)(y - 5) +(y - 5)², если у = 3,5
б) Решите уравнение (3x + 2)2 - (3x-5)(3x + 5) = 23
в) Решите неравенство 2х (8х + 3) + 1 < (5 - 4x)2 - 1
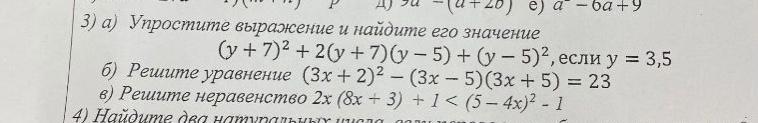
Ответы на вопрос
Ответ:
Объяснение:
a) Выполним подстановку значения y = 3,5 и вычислим выражение:
(y+7)2 + 2(y +7)(y - 5) +(y - 5)² = (3.5+7)² + 2(3.5+7)(3.5-5) +(3.5-5)²
= 10.5² + 2(10.5)(-1.5) + (-1.5)²
= 110.25 - 31.5 + 2.25
= 81
Таким образом, при y = 3,5 значение выражения равно 81.
б) Решим уравнение (3x + 2)² - (3x-5)(3x + 5) = 23:
(3x + 2)² - (3x-5)(3x + 5) = 23
9x² + 12x + 4 - (9x² - 25) = 23
36x = 44
x = 11/9
Таким образом, решением уравнения является x = 11/9.
в) Решим неравенство 2х(8х + 3) + 1 < (5 - 4x)² - 1:
2х(8х + 3) + 1 < (5 - 4x)² - 1
16x² + 6x + 1 < 25 - 40x + 16x² - 1
46x < 25
x < 25/46
Таким образом, решением неравенства является x < 25/46.
a)
(3,5 + 7)² + 2(3,5 + 7)(3,5 - 5) + (3,5 - 5)² = (10,5)² + 2(10,5)(-1,5) + (-1,5)² = 110,25 - 31,5 + 2,25 = 81
б)
Почнемо розв'язування рівняння:
(3x+2)² - (3x-5)(3x+5) = 23
Розкриваємо дужки в другому доданку:
(3x+2)² - (9x² - 25) = 23
Розкриваємо перше доданок за допомогою формули квадрату двохчлену:
9x² + 12x + 4 - 9x² + 25 = 23
Скорочуємо подібні доданки:
12x + 29 = 23
Віднімаємо від обох сторін 29:
12x = -6
Ділимо на 12:
x = -0,5
Отже, розв'язком рівняння є x = -0,5.
в)
Почнемо розв'язування нерівності:
2x(8x + 3) + 1 < (5 - 4x) - 1
Розкриваємо дужки в обох доданках:
16x² + 6x + 1 < 4 - 4x
Переносимо всі доданки на одну сторону:
16x² + 10x - 3 < 0
Тепер треба знайти корені квадратного тричлена 16x² + 10x - 3:
x₁,₂ = (-b ± √(b² - 4ac)) / 2a
де a = 16, b = 10, c = -3.
x₁,₂ = (-10 ± √(10² - 4·16·(-3))) / 2·16
x₁,₂ = (-10 ± √(100 + 192)) / 32
x₁,₂ = (-10 ± √292) / 32
x₁ ≈ -0,5662 або x₂ ≈ 0,1912.
Отже, розв'язком нерівності є проміжок (-∞, -0.5662) об'єднаний з проміжком (0.1912, +∞).