Алгебра, вопрос задал prototypbox , 6 лет назад

100 баллов помогите пожлайста!!! алгебра

Приложения:

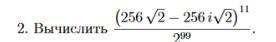
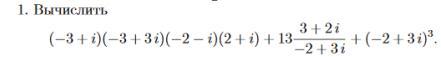
Ответы на вопрос

Ответил NNNLLL54

Ответ:

$1)\ \ \dfrac{(256\sqrt2-256\, i\, \sqrt2)^{11}}{2^{99}}=\dfrac{(256\cdot \sqrt2)^{11}(1-i)^{11}}{2^{99}}=\dfrac{2^{88}\cdot 2^{5,5}\cdot (1-i)^{11}}{2^{99}}=\\\\=2^{-5,5}\cdot (1-i)^{11}$

Запишем комплексное число в тригонометрической форме , так как в степень удобно возводить компл. число именно в триг. форме .

$z=1-i\ \ \Rightarrow \ \ \ r=\sqrt{1^2+(-1)^2}=\sqrt2\ \ ,\ \ \varphi \in (-\pi\, ;\, \pi \ )\ ,\\\\{}\ \ \ \ \ \varphi =arg\, z=arctg\dfrac{b}{a}=arctg\dfrac{-1}{1}=-\dfrac{\pi }{4}\\\\{}\quad \ \ z=(1-i)=\sqrt2\, \Big(cos(-\dfrac{\pi }{4})+i\, sin(-\dfrac{\pi}{4})\, \Big)\\\\z^{11}=(\sqrt2)^{11}\, \Big(cos(-\dfrac{11\pi }{4})+i\, sin(-\dfrac{11\pi }{4})\, \Big)=2^{5,5}\, \Big(cos(-\dfrac{3\pi}{4})+i\, sin(-\dfrac{3\pi }{4})\Big)$

$\star \ 2^{-5,5}\cdot (1-i)^{11}=2^{-5,5}\cdot 2^{5,5}\Big(cos(-\dfrac{3\pi}{4})+i\, sin(-\dfrac{3\pi}{4})\Big)=cos(-\dfrac{3\pi}{4})+i\, sin(-\dfrac{3\pi}{4})$

$2)\ \ (-3+i)(-3+3i)(-2-i)(2+i)+13\cdot \dfrac{3+2i}{-2+3i}+(-2+3i)^3$

Выполняем действия с комплексными числами, учитывая, что $i^2=-1$ .

$\star \ (-3+i)(-3+3i)=9-9i-3i+3i^2=6-12i\\\\(-2-i)(2+i)=-(2+i)(2+i)=-(4+4i+i^2)=-(3+4i)\\\\-(6-12i)(3+4i)=-(18+24i-36i-48i^2)=-(66-12i)=\underline {-66+12i\ }\\\\\\\star \ \dfrac{3+2i}{-2+3i}=\dfrac{3+2i}{-(2-3i)}=\dfrac{(3+2i)(2+3i)}{-(2-3i)(2+3i)}=-\dfrac{6+13i-6}{4+9}=-\dfrac{13i}{13}=\underline{\, -i\, }$