Алгебра, вопрос задал Algebroidka , 1 год назад

100 баллов. Объясните. Тоже не сходится ничего
Ответ должен быть от минус бесконечности до -5/4. и от 0 до 4

Приложения:

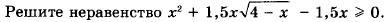
Algebroidka: может тогда в ответах ошибка

Ответы на вопрос

Ответил Аноним

1

$x^2+1.5 x\sqrt{4-x} -1.5x \geq 0$

Рассмотрим функцию
$y=x^2+1.5 x\sqrt{4-x} -1.5x$
Область определения функции: $4-x \geq0\to x \leq 4$
$D(y)=(-\infty;4]$

Приравняем функцию к нулю
$y=0 \\ x^2+1.5x \sqrt{4-x} -1.5x=0$
$x(x+1.5 \sqrt{4-x} -1.5)=0 \\ x_1=0 \\ \\ x+1.5 \sqrt{4-x} -1.5=0$

$1.5 \sqrt{4-x} =-x+15$
Возведем оба части до квадрата
$(1.5 \sqrt{4-x})^2 =(-x+15)^2 \\ 2.25(4-x)=x^2-3x+2.25=0 \\ x^2-0.75x-6.75x=0|\cdot 4 \\ 4x^2-3x-27=0 \\ D=b^2-4ac=(-3)^2-4\cdot 4\cdot (-27)=441; \sqrt{D} =21 \\ x_1=- \frac{9}{4} \\ x_2=3$

__+_[-9/4]__-__[0]__+__[3]___+___[4]

Ответ: $(-\infty;- \frac{9}{4} ]\cup [0;4]$

Algebroidka: все значения на одной числовой прямой? у меня другой промежуток получается

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Қазақ тiлi, 1 год назад

ПОМОГИТЕ ПОЖАЛУЙСТА!!!!!!! ДАЮ 20 БАЛЛОВ...

Английский язык, 1 год назад

Put the verbs in brackets into the present simple or present continuous. 1 He ofter goes(go) to the cinema. И всю страну пожалуйста помогите я дам 15 баллов...

Математика, 1 год назад

Иван Иванович хочет доехать на машине от г.Минска до г.Москвы через Смоленск и Вязьму. Он выяснил, что расстояние от Минска до Смоленска 366 км, от Минска до Вязьмы - 478 км. Путь от Москвы до...

Математика, 1 год назад

Перед ремонтом зоопарка животных вывезли в специальных автофургонах, Было сделано 150 рейсов. Каждым рейсом отправлялось одно и тоже количество животных. После ремонта зоопарка сделали 170 таких же...

Музыка, 7 лет назад

я хочу ноти береги мое сердце будь мо мной...

Математика, 7 лет назад

Площадь поля 75 га. В 1 день засеяли 24% свей площади. Сколько га осталось засеять?