100 БАЛІВ ДАЮ!!!!!!!
Знайти критичні точки !!!!! Срочно!!!!
Картка #2
Якшо можна то ще знайти екстримуми функції двже потрібно

Ответы на вопрос
Критические точки - внутренние точки области определения, в которых производная равна нулю или не существует. находим эти точки после нахождения производной.
у'=4x³-6x²=0
2x²(2x-3)=0
Критические точки х=0, х=1.5
разобьем этими точками область определения на промежутки и выясним знак производной на каждом из них.
______0________1.5______
- - +
точка х=0 не является точкой экстремума, х=1.5- точка минимума, минимум равен у(1.5)= (3/2)⁴-2*(3/2)³-3=81/16-54/8-3=5.0625-6.75-3=-4.6875
Картка #2
Якшо можна то ще знайти екстримуми функції двже потрібно
Ответ:
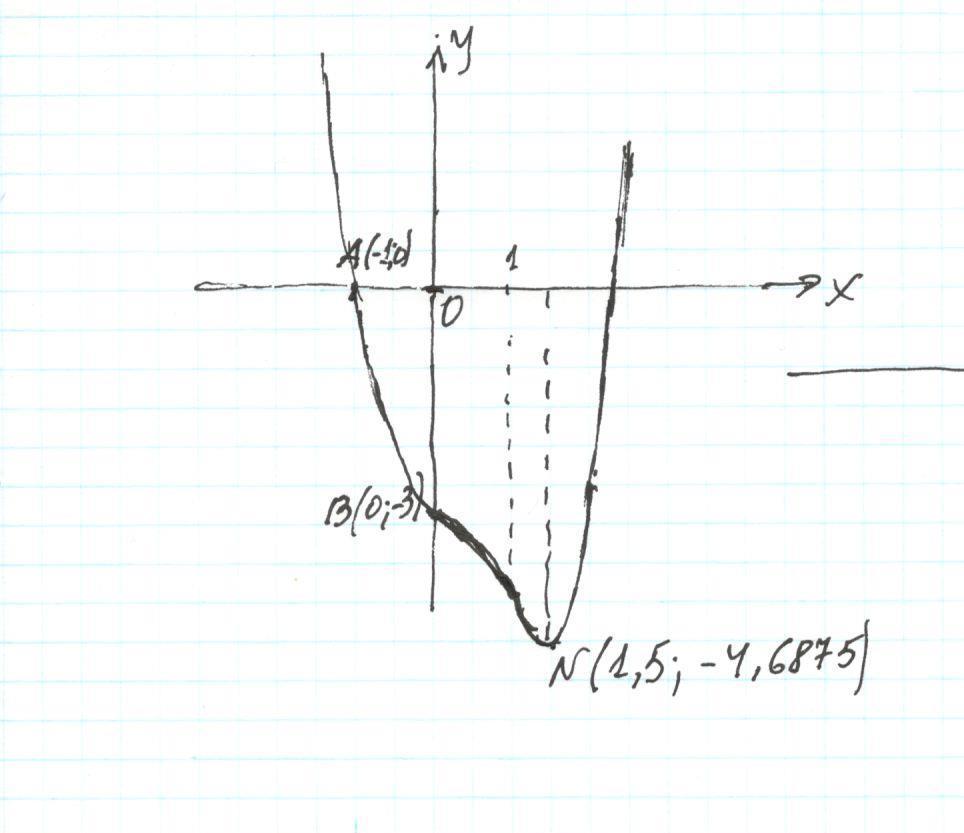
Исследовать функцию y = x⁴ -2x³ -3 и построить ее график
( Если можно то еще найти экстремумы функции очень нужно )
Объяснение: y(x) = x⁴ -2x³ - 3
1. OOФ : x ∈ R || x∈ ( - ∞ ; ∞ )
2. Функция не четная , не нечетная , не периодическая
3. Пересечения с осями координат
С осью абсцисс : y = 0 ; x⁴- 2x³- 3 =0 целое решение x = - 1
(x+1)(x³ - 3x² +3x -3) = 0 A( - 1 ; 0)
x³ - 3x² +3x - 3 =0 не имеет целое решение , c помощью графики найдем еще одно x ≈ 2,26 ( остальные 2 мнимые)
С осью ординат: x = 0 ; y = - 3 B ( 0 ; - 3)
4. Определим области возрастания и убывания функции
y'(x) = (x⁴ -2x³ -3 ) ' = 4x³ - 6x² = 4x²(x -3/2 )
Стационарные точки : y '(x) =0 ⇔ 4x²(x -3/2) =0 ⇒ [x =0 ; x =3/2
y'(x) ( - ∞ ) - - - - - - - [0] - - - - - - - [3/2] + + + + + + + +
y(x) ↓ ↓ min ↑
Стационарная точка x = 0 не является точкой экстремума , поскольку при переходе через эту точку производная функции не меняет свой знак .
При переходе через стационарную точку x = 3/2 производная функции меняет знак, с «минуса» на «плюс», значит эта точка является точкой минимума
функция убывает при x ∈ ( -∞ ; 3/2 ]
функция возрастает при x∈ [3/2 ; ∞ )
Минимальное значение y(3/2) =(3/2)⁴- 2*(3/2)³- 3 =81 /16 - 27/4 - 3=
(81 -108 -48) /16 =-75/16 = - 4,6875 N ( 1,5 ; - 4,6875)
5. Определим точки перегибов ( из y'' = 0 ) :
у' ' (x) = ( y'(x) ) ' = (4x³ - 6x²) ' = 12x²-12x =12x(x-1)
у' ' (x) =0 ⇔ 12x(x-1) =0 ⇔ [ x = 0 ; x=1 . точки перегиба
у' ' (x) + + + + + + + [0] - - - - - - [1] + + + + + + + +
График функции вогнутая, если x ∈ (-∞ ; 0) и x ∈ ( 1 ; ∞ )
График функции выпуклая , если x ∈ ( 0; 1 ) .