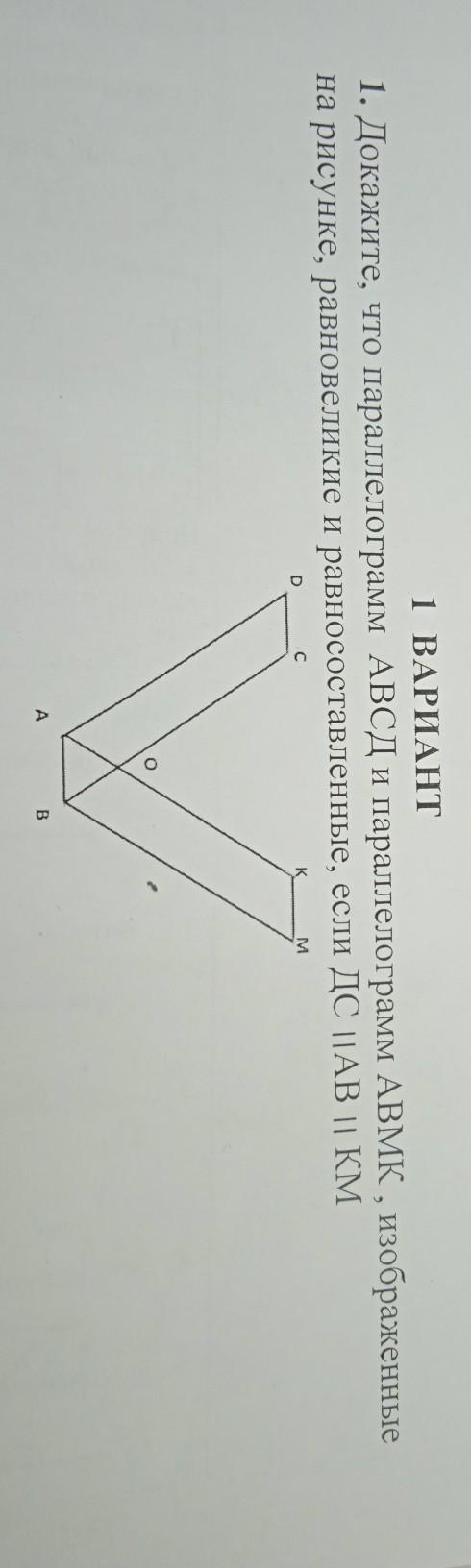
1 ВАРИАНТ 1. Докажите, что параллелограмм АВСД и параллелограмм ABMK , изображенные на рисунке, равновеликие и равносоставленные, если ДС ПАВ || KM D с K M A В​

Ответ:

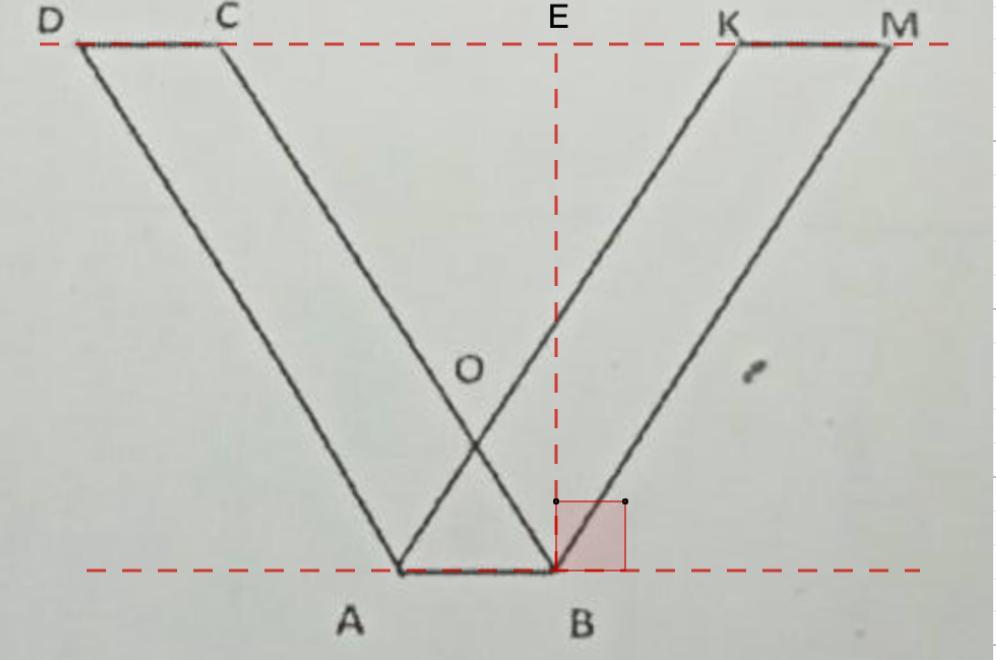
Параллелограмм АВСD и параллелограмм ABMK , изображенные на рисунке, равновеликие и равносоставленные.

Объяснение:

Требуется доказать, что параллелограмм АВСD и параллелограмм ABMK , изображенные на рисунке, равновеликие и равносоставленные.

Дано: параллелограмм АВСD и параллелограмм ABMK.

DC || AB || KM.

Доказать: АВСD и ABMK.

Решение:

Доказательство:

• Равновеликие фигуры - это плоские фигуры, у которых площади равны.

Проведем DM и убедимся, что DC и КМ находятся на одной прямой.

Проведем высоту ЕВ.

Это высота является высотой для двух параллелограммов.

АВ - основание АВСD и ABMK.

• Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.

S (АВСD) = S (ABMK) = AB · EB.

⇒ АВСD и ABMK - равновеликие фигуры.

• Любые два равновеликих многоугольника равносоставлены.

⇒ Параллелограмм АВСD и параллелограмм ABMK , изображенные на рисунке, равновеликие и равносоставленные.