1)В трапеции ABCD AB=BC=CD. Точки K,L,M и N - середины сторон трапеции. Найдите наибольший угол четырёхугольника KLMN, если угол BAD равен 40∘. Ответ дайте в градусах.
2) В стакане с ручками стоят 6 ручек, которые еще пишут, и 4 ручки, которые уже не пишут. Случайно выбирается одна ручка, с какой вероятностью она пишет?
3)Дана арифметическая прогрессия y1=−323,y2=−113,… Найдите сумму первых шести членов этой прогрессии.
4)Диагонали ромба равны 24 и 7,5. Найдите его площадь.
5)
Какие из следующих утверждений верны? В любой прямоугольный треугольник можно вписать окружность. Каждая сторона треугольника больше суммы двух других сторон. В треугольнике ABC угол A равен 43∘, угол C равен 72∘,AC - меньшая сторона. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы. Любые два равнобедренных треугольника подобны.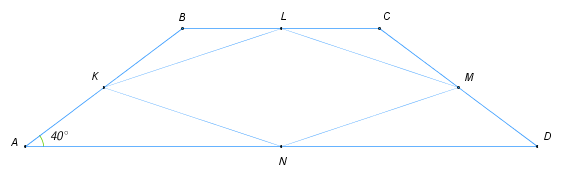
Ответы на вопрос
К задаче №1.
1) KB=BL (так как AB=BC и точки K и L - середины)
2) угол ABC=140 градусов (т.к. сумма углов при боковой стороне трапеции 180) (180-40=140)
3) угол KLB=углу BKL=20 градусов (свойство равнобедренного треугольника) (180-140)/2=20
4) треугольник LCM=треугольнику KBL (по 1-му признаку и п.1)
5) Наибольший угол KLMN равен 180-2*20=140
Этот четырёхугольник является ромбом, т.к. KL=LM=MN=NA (это средние линии треугольников ABC и ADC)
К задаче №3.
1) найдём d=y2-y1=-113+323=210
2) По формуле суммы n членов арифметической прогрессии:
S(6)=6*(2*(-323)+210*5)/2=1212
К задаче №4.
1) Воспользуйтесь формулой S ромба=(1/2)*d1*d2, получим 24*7,5/2=90
К задаче №5.
Верными являются утверждения №1 и 4