1 В прямоугольном треугольнике один из острых углов на 26° больше другого. Чему равны острые
углы этого треугольника?
2. Периметр равнобедренного треугольника равен 26 см, разность двух сторон равна 5 см, а один из
его внешних углов — острый. Найдите стороны треугольниа​

Объяснение:

один угол ▪︎х°

другой угол ▪︎(х+26)°

Два острых угла в прямоугольном треугольнике ▪︎90°

х + х + 26 = 90

2х = 90 - 26

2х = 64 |÷2

х = 32° один острый угол

32 + 26 = 58° другой острый угол

нр.2

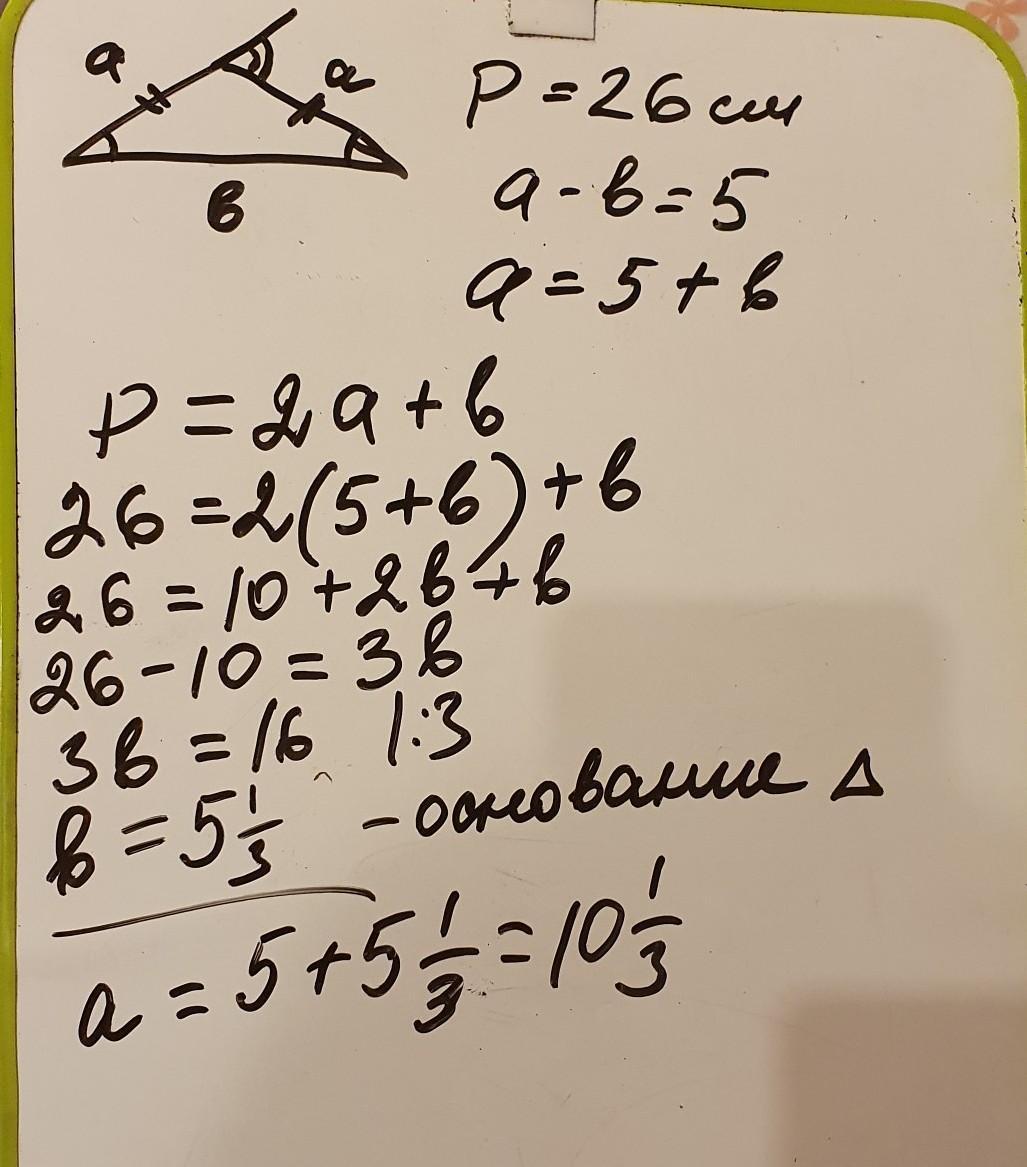
смотри фото. Написала два варианта решения, т.к. не сказано, какая сторона больше, боковая или основание, поэтому разность сторон можно понимать в двух вариантах: от боковой стороны отнимают основание и наоборот. Но мне второй вариант нравится больше, т.к. числа нормальные выходят, а не дробные.

А по поводу угла, если один внешний угол острый, то это может быть только угол при вершине, т.к. в треугольнике соответственно угол будет тупой. А тупой угол в треуголнике может быть только один. А в равнобедренном треугольнике углы при основании равны.