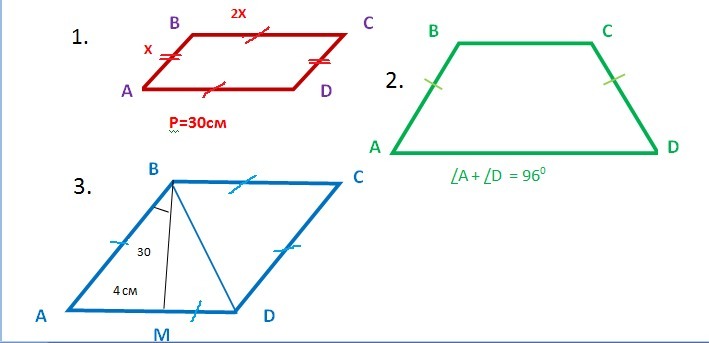
1)Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. найдите стороны параллелограмма.
2) В равнобокой трапеции сумма углов при большем основании равно 96 градусов. найдите углы трапеции.
3)Высота ВМ, проведенная из вершины угла ромба АВСD образует со стороной АВ угол 30 градусов, АМ= 4 см. найдите длину диагонали ВD ромба,если точка М лежит на стороне АD
СКАЖИТЕ ЕЩЕ ПОЖАЛУЙСТА ЧТО НАДО ЧЕРТИТЬ ОЧЕНЬ НАДО!СПАСИБО)
Ответы на вопрос
Ответил helenaal
0
1.
Дано: АВСД - пар-м
АВ : ВС = 1 : 2
Р = 30 см
Найти: AB; BC; CD; AD
Решение.
Пусть АВ = Х, тогда ВС = 2Х, т.к. по условию АВ : ВС =1 : 2
В параллелограмме противоположные стороны равны.
АВ = CD = X BC = AD = 2X
P = AB + BC + CD + AD = Х + 2Х + Х + 2Х = 6Х = 30 (см)
Х = 30 : 6 = 5 (см)
2Х = 5 * 2 = 10 (см)
Ответ: АВ и CD = 5 см; ВС и АD = 10 см
2.
Дано: АВСД - тр-я
АВ = СD
∠А + ∠D = 96°
Найти: ∠А ; ∠В; ∠С; ∠D
Решение.
Т.к. по условию трапеция равнобокая, углы при основаниях равны, т.е. каждый равен их полусумме.
Углы при большем основании ∠А = ∠D = (∠A + ∠D)/2 = 96° : 2 = 48°
∠А + ∠В = 180° как углы прилежащие к одной боковой стороне
∠В = 180° - 48° = 132 °, но ∠В = ∠С
Ответ: ∠А =∠D = 48°; ∠В = ∠С = 132°
3.
Дано: АВСD - ромб
ВМ ⊥ АD
∠АВМ = 30°
АМ = 4 см
Найти: ВМ
Решение.
Δ АВМ - прямоугольный, ∠АМВ = 90, т.к. ВМ - высота
АВ - гипотенуза, АМ - катет, лежащий против ∠АВМ = 30°, следовательно, АВ = 2 АМ = 8 (см) и ∠ВАМ = 90° - 30° = 60°
Т.к. у ромба все стороны равны, то АВ = АD
Рассмотрим ΔАВD. Т.к. АВ = АD, значит, равны и углы при основании равнобедренного тр-ка : ∠АВD = ∠АDВ = (180° - 60°)/2 = 60° ⇒
ΔАВD - равносторонний, ВD = АВ = АD = 8 (cм)
Ответ: ВD = 8 см
Дано: АВСД - пар-м
АВ : ВС = 1 : 2
Р = 30 см
Найти: AB; BC; CD; AD
Решение.
Пусть АВ = Х, тогда ВС = 2Х, т.к. по условию АВ : ВС =1 : 2
В параллелограмме противоположные стороны равны.
АВ = CD = X BC = AD = 2X
P = AB + BC + CD + AD = Х + 2Х + Х + 2Х = 6Х = 30 (см)
Х = 30 : 6 = 5 (см)
2Х = 5 * 2 = 10 (см)
Ответ: АВ и CD = 5 см; ВС и АD = 10 см
2.
Дано: АВСД - тр-я
АВ = СD
∠А + ∠D = 96°
Найти: ∠А ; ∠В; ∠С; ∠D
Решение.
Т.к. по условию трапеция равнобокая, углы при основаниях равны, т.е. каждый равен их полусумме.
Углы при большем основании ∠А = ∠D = (∠A + ∠D)/2 = 96° : 2 = 48°
∠А + ∠В = 180° как углы прилежащие к одной боковой стороне
∠В = 180° - 48° = 132 °, но ∠В = ∠С
Ответ: ∠А =∠D = 48°; ∠В = ∠С = 132°
3.
Дано: АВСD - ромб
ВМ ⊥ АD
∠АВМ = 30°
АМ = 4 см
Найти: ВМ
Решение.
Δ АВМ - прямоугольный, ∠АМВ = 90, т.к. ВМ - высота
АВ - гипотенуза, АМ - катет, лежащий против ∠АВМ = 30°, следовательно, АВ = 2 АМ = 8 (см) и ∠ВАМ = 90° - 30° = 60°
Т.к. у ромба все стороны равны, то АВ = АD
Рассмотрим ΔАВD. Т.к. АВ = АD, значит, равны и углы при основании равнобедренного тр-ка : ∠АВD = ∠АDВ = (180° - 60°)/2 = 60° ⇒
ΔАВD - равносторонний, ВD = АВ = АD = 8 (cм)
Ответ: ВD = 8 см
Приложения:
Новые вопросы