1. Спрости цілий вираз. a) 2ab(3 – 2а) + 4b(За – 7a²); - B) x(x² - y²) + y(xу – y²); - б) г) (x - 2y) · 2ху - 28х²у, - - (2х - 2а)(3а² - 4а + 5). -
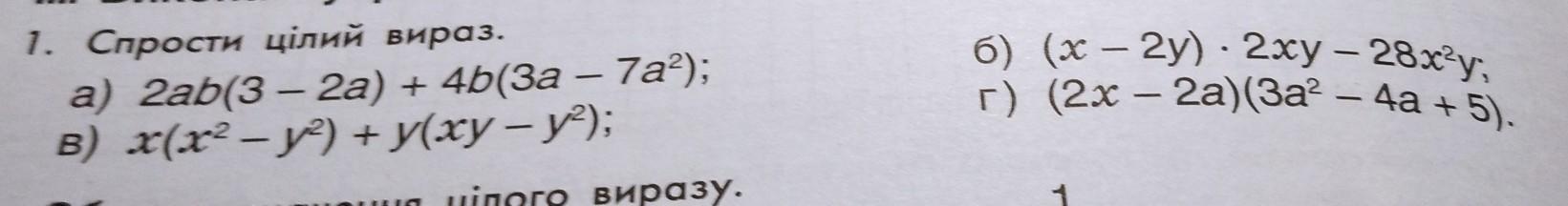
Ответы на вопрос
Ответ и Объяснение:
Требуется упростить целое выражение.
a) 2·a·b·(3 – 2·a) + 4·b·(З·a – 7·a²);
б) (x – 2·y) · 2·x·y – 28·x²·y
в) x·(x² – y²) + y·(x·y – y²);
г) (2·x – 2·a)·(3·a² – 4·a + 5).
Информация. Правила раскрытия скобок:
1) Чтобы раскрыть скобки, перед которыми стоит знак " - ", надо заменить этот знак на " + ", поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки. Если перед скобками стоит +. то при раскрытии скобок слагаемые сохраняют свои знаки.
2) Если перед скобками стоит знак умножения, то каждое число, стоящее внутри скобок, умножается на множитель, стоящий перед скобками. Общие формулы:
a·(-b+c-d) = -a·b+a·c-a·d, -a·(-b+c-d) = a·b-a·c+a·d.
Решение. Раскроем скобки и приведём подобные слагаемые (подобные слагаемые отметим одинаковым шрифтов).
a) 2·a·b·(3 – 2·a) + 4·b·(З·a – 7·a²) = 6·a·b – 4·a²·b + 12·a·b – 28·a²·b =
= 18·a·b – 32·a²·b;
б) (x – 2·y) · 2·x·y – 28·x²·y = 2·x²·y – 4·x·y² – 28·x²·y = – 4·x·y² – 26·x²·y;
в) x·(x² – y²) + y·(x·y – y²) = x³ – x·y² + x·y² – y³ = x³ – y³;
г) (2·x – 2·a)·(3·a² – 4·a + 5) = 6·x·a² – 8·x·a + 10·x – 6·a³ + 8·a² – 10·a.
#SPJ1