1)Очень нужен рисунок ребят
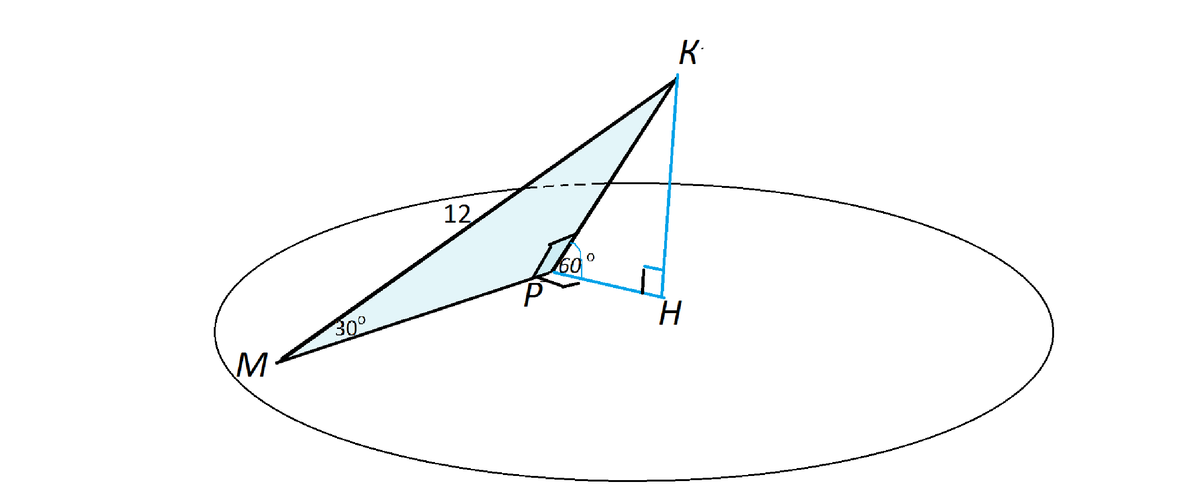
В треугольнике MKP MK = 12 см, угол М = 30, угол Р = 90. Плоскость а проходит через сторону MP и образует с плоскостью MKP 60 градусов. Найдите расстояние от точки К до плоскости а.
2)Очень нужен рисунок ребят
Плоскость B проходит через сторону MN треугольника MKN.Сторона KN образует с плоскостью B угол 30гр.Найдите синус угла между плоскостями B и MKN,если MK=12см,KN=13см,MN=5см
Ответы на вопрос
Ответил Hrisula
0
1) В треугольнике MKP MK = 12 см, угол М = 30°, угол Р = 90° Плоскость α роходит через сторону MP и образует с плоскостью MKP 60°. Найдите расстояние от точки К до плоскости α.
Расстояние от точки до плоскости измеряют перпендикулярным отрезком.
Это отрезок КН прямоугольного треугольника КРН. КР, противолежащая углу 30° треугольника КРМ, равна половине КМ и равна 6 см.
КН=КР*sin ∠КРН=КР*sin (60)=3√3
2)
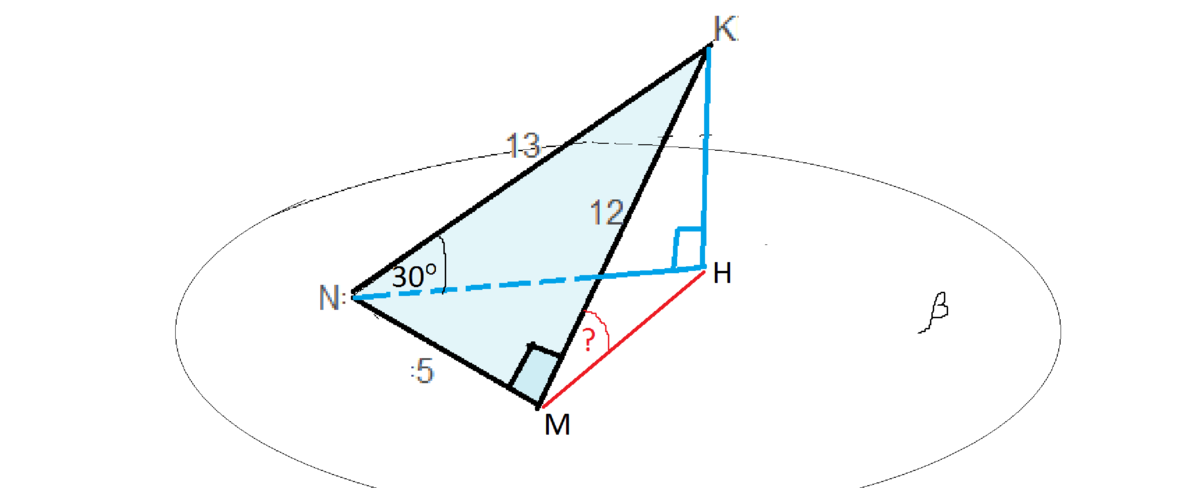
Плоскость β проходит через сторону MN треугольника MKN. Сторона KN образует с плоскостью β угол 30°. Найдите синус угла между плоскостями β и MKN, если MK=12см, KN=13см, MN=5см
Обратим внимание на отношение сторон треугольника -12:13:5. Это отношение прямоугольного треугольника из Пифагоровых троек. ( Можете проверить).
Точка К проецируется на плоскость β в точке Н, а КН перпендикулярна β . Из треугольника КNH найдем КН .
Она равна половине КH как катет, противолежащий углу 30°
Т.к. наклонная КМ перпендикулярна МN, то ее проекция также перпендикулярна МN.
Угол. синус которого надо найти, ограничен отрезками КМ и МН.
Т.е. это угол КМН.
sin ∠КМН=KH:KM=6,5:12=0,541(6)
-----------
[email protected]
Расстояние от точки до плоскости измеряют перпендикулярным отрезком.
Это отрезок КН прямоугольного треугольника КРН. КР, противолежащая углу 30° треугольника КРМ, равна половине КМ и равна 6 см.
КН=КР*sin ∠КРН=КР*sin (60)=3√3
2)
Плоскость β проходит через сторону MN треугольника MKN. Сторона KN образует с плоскостью β угол 30°. Найдите синус угла между плоскостями β и MKN, если MK=12см, KN=13см, MN=5см
Обратим внимание на отношение сторон треугольника -12:13:5. Это отношение прямоугольного треугольника из Пифагоровых троек. ( Можете проверить).
Точка К проецируется на плоскость β в точке Н, а КН перпендикулярна β . Из треугольника КNH найдем КН .
Она равна половине КH как катет, противолежащий углу 30°
Т.к. наклонная КМ перпендикулярна МN, то ее проекция также перпендикулярна МN.
Угол. синус которого надо найти, ограничен отрезками КМ и МН.
Т.е. это угол КМН.
sin ∠КМН=KH:KM=6,5:12=0,541(6)
-----------
[email protected]
Приложения:
Новые вопросы