1)Найдите значения х,при которых трехчлен -16x^2+8x-1 принимает отрицательные значения. 2)докажите,что при любом значении а верно неравенство: 6а<а^2+10
Ответы на вопрос
1)Найдите значения х,при которых трехчлен -16x^2+8x-1 принимает отрицательные значения.
-16x^2+8x-1=-(16x^2-8x+1)=-(4x-1)^2
(4x-1)^2 - всегда дает положительное значение кроме x=1/4
- (4x-1)^2 - всегда дает отрицателное значение кроме x=1/4
Ответ x (-∞;1/4) U (1/4; +∞)
2)докажите,что при любом значении а верно неравенство:
6а<а^2+10
0<а^2-6a+10
0<а^2-6a+9+1
0<а^2-6a+3^2+1
0<(а-3)^2+1
(а-3)^2 - положительное при любом a
значит (а-3)^2+1 - положительное при любом а
значит при любом значении а верно ИСХОДНОЕ неравенство
ДОКАЗАНО
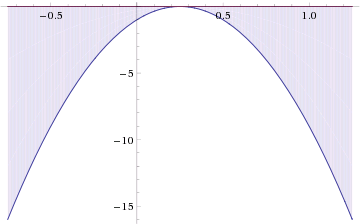
1) -16x^2+8x-1<0
домножаем на -1 -> меняем знак неравенства
16x^2+8x-1>0
преобразуем
(4х-1)^2>0
данное равенство верно всегда кроме, случая когда x=1/4 -> изначальное условие принимает отрицательное значение везде кроме точки х=1/4
2) переносим все части неравенства в одну сторону
a^2-6x+10>0
D=36-40<0 -> уравнение не имеет корней -> функция всегда больше нуля
