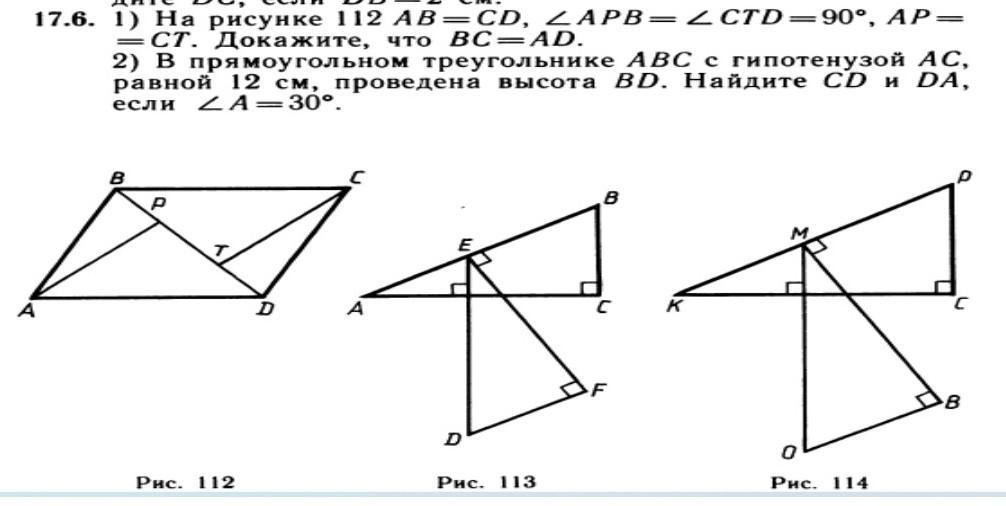
1)на рисунке 112 AB=CD, APB=CTD=90⁰, AP=CT.Докажите что BC=AD.
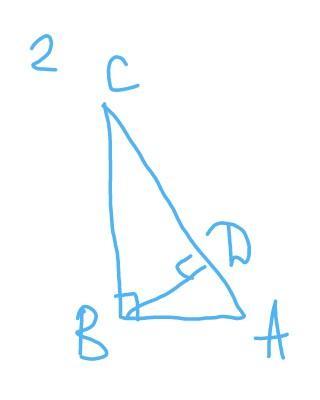
2)в прямоугольном треугольнике ABC с гипотенузой AC, равной 12 см,проведена высота BD. Найдите CD и DA, если A=30⁰
За решение двух вопросов дам 30 баллов! ​

Ответ:

112

1

Рассмотрим тр-к АВР и тр-к СDT:

<APB=<CTD=90 градусов, тр-ки прямоугольные

АВ=СD

AP=CT

Тр-ки равны по гипотенузе и катету,значит

соответственные элементы равны :

ВР=TD

BT=BD-TD

|| ||

DP=BD-BP, значит ВТ=DP

Рассмотрим тр-к АРD и тр-к СТB:

<APD=<CTB=90 градусов

AP=CT

DP=BT

Тр-ки равны по двум катетам,значит соответствующие элементы равны, следовательно, ВС=АD

2

Тр-к АВС ; <В=90 градусов

АС=12 см

<A=30 градусов

Найти : СD и DA

Рассмотрим тр-к АВС:

<С=90-<А=90-30=60 градусов

Катет лежащий против угла 30 равен половине гипотенузе :

ВС=АС:2=12:2=6 см

Рассмотрим тр-к ВCD :

<CDB=90 градусов,

соs<C=CD/BC

CD=BC×cos60=6×1/2=3 cм

DA=AC-CD=12-3=9 cм

Ответ : СD=3 cм ; DA=9 cм

2 способ:

Рассмотрим тр-к АВС:

<А=30 градусов

Катет лежащий против угла 30 равен половине гипотенузе :

ВС=АС:2=12:2=6 см

По теореме Пифагора :

АС^2=АВ^2+ВС^2

АВ^2=АС^2-ВС^2=12^2-6^2=

=144-36=108

АВ=корень 108=корень (36×3)=

=6корень3 (см)

Рассмотрим тр-к АВD - прямоугольный

<А=30 градусов :

Катет лежащий против угла 30 равен половине гипотенузе :

ВD=AB :2=6корень3 :2=

=3корень3 (см)

По теореме Пифагора :

DA^2=AB^2-BD^2

DA^2=(6корень3)^2-(3корень3) ^2=

=36×3-9×3=108-27=81

DA=корень 81=9 см

СD=AC-DA=12-9=3 cм

Ответ : СD=3 cм ; DA=9 cм