№1
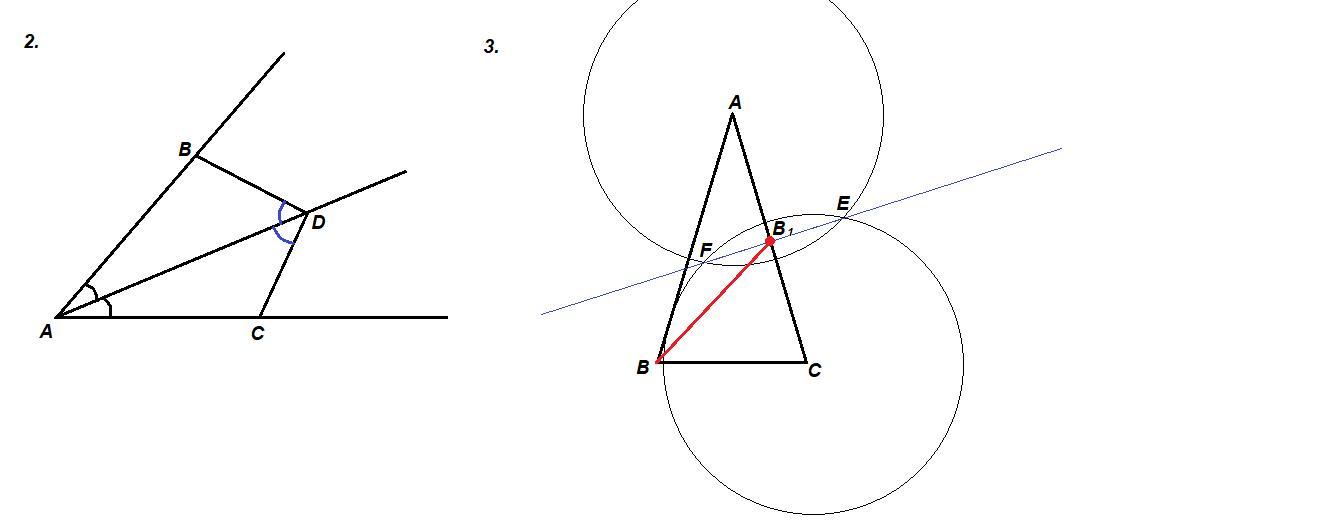
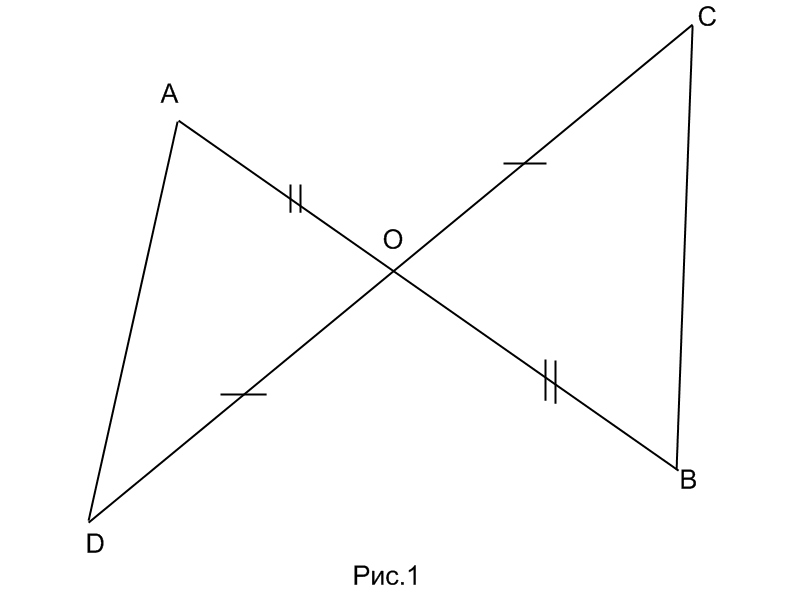
На рисунке 1(он прикреплён)отрезки АВ и CD имеют общую середину О.Докажите,что угол DAO=углу CBO.
№2
Луч AD-биссектриса угла А.На сторонах угла А отмечены точки В и С так,что угол ADB=углу ADC.Докажите , что АВ=АС.
№3
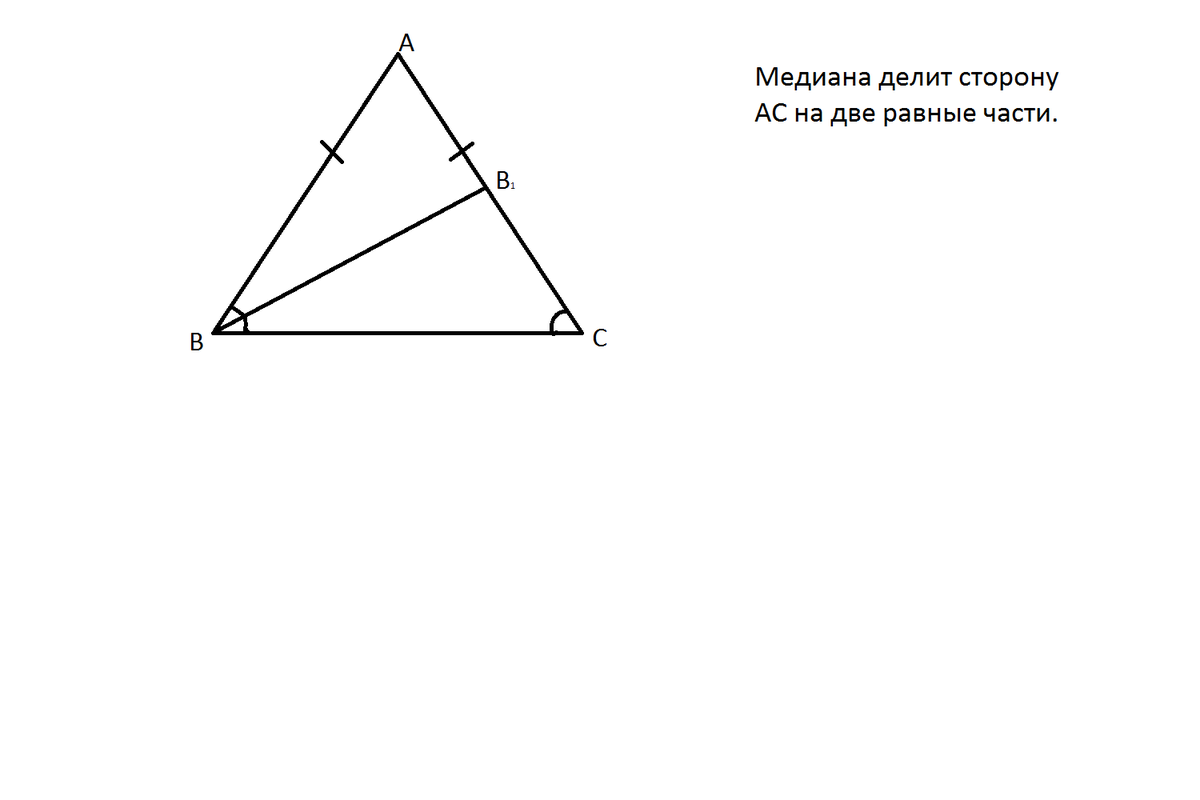
Начертите равнобедренный треугольник АВС с основанием ВС.С помощью циркуля и линейки проведите медиану ВВ₁ к боковой стороне АС.
Ответы на вопрос
2)Угол А-общий, Если мы соединим В и С с точкой D, образуются два треугольника
ABD и ADC. Дальше приводим признак равенства треугольников:
Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. В данном случае AD-общая сторона, угол А делится пополам, угол ADB=углу ADC, следовательно треугольники равны. AD=AC соответственно.
3)
Ответ:
1. АО = ОВ и СО = OD, так как О - середина отрезков АВ и CD,
∠АОD = ∠ВОС как вертикальные, ⇒
ΔAOD = ΔBOC по двум сторонам и углу между ними.
В равных треугольниках напротив равных сторон лежат равные углы, следовательно ∠DAO = ∠CBO.
2. ∠BAD = ∠CAD, так как AD - биссектриса угла А,
∠ADB = ∠ADC по условию,
AD - общая сторона для треугольников ADB и ADC, значит
ΔADB = ΔADC по стороне и двум прилежащим к ней углам.
В равных треугольниках напротив равных углов лежат равные стороны, значит АВ = АС.
3. Для построения медианы ВВ₁ надо построить середину отрезка АС.
1) Проведем две окружности с одинаковым произвольным радиусом (большим половины стороны АС) с центрами в точках А и С.
Точки пересечения окружностей Е и F.
2) Проведем прямую EF.
Точка пересечения прямой EF и стороны АС - B₁.
В₁ - середина стороны АС.
3) Проведем отрезок ВВ₁.
ВВ₁ - искомая медиана.