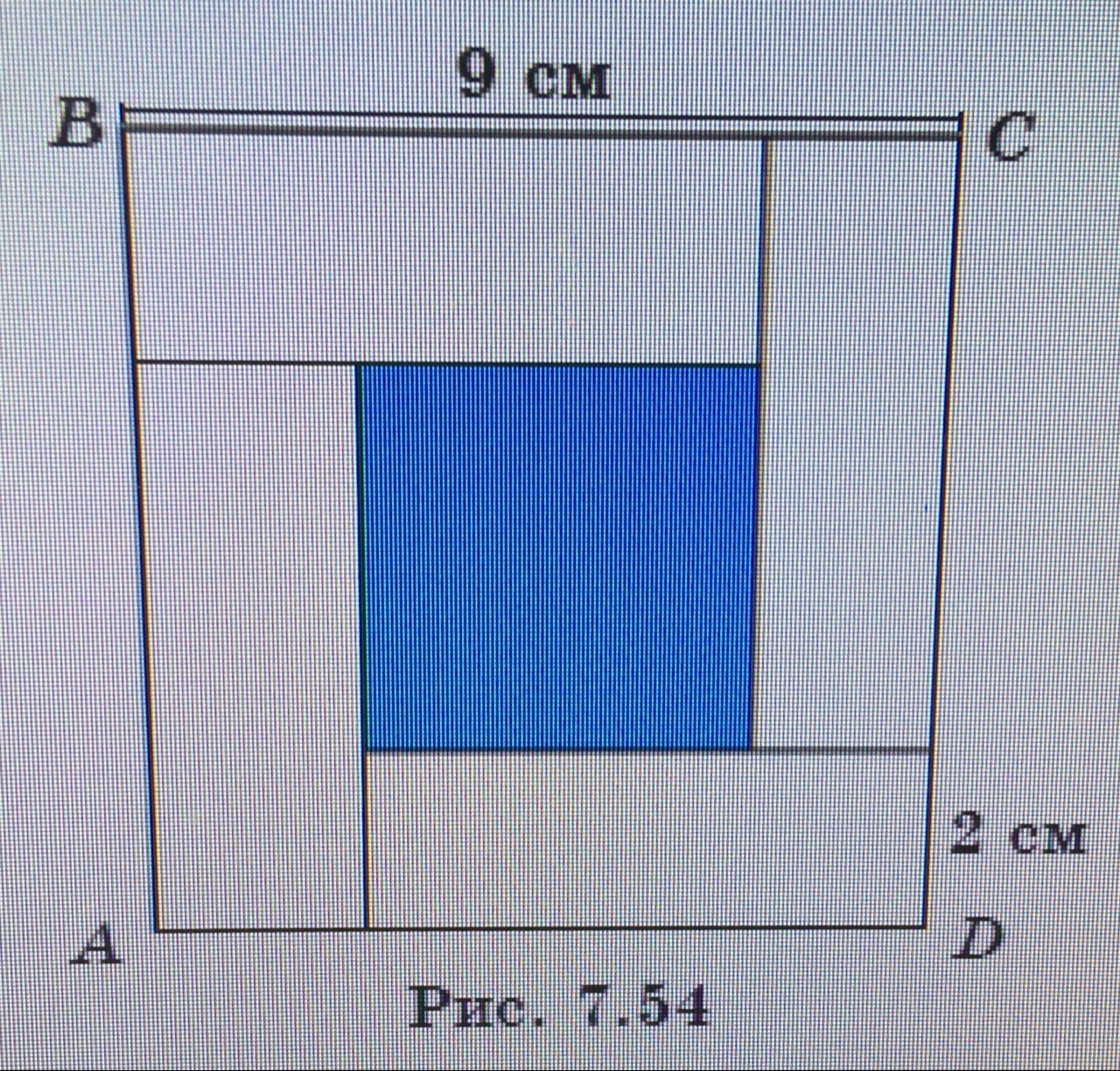
1) Какие многоугольники изображены на рисунке 7.54?
2) Найдите периметр закрашенной части многоугольника ABCD.
3) Найдите площадь незакрашенной части многоугольника ABCD.
Ответы на вопрос
1) На рисунке посередине синим цветом выделен квадрат. Вокруг него располагаются четыре равных прямоугольника. АВСD - квадрат.
2) Закрашенная часть это квадрат. Длина его стороны равна длине квадрата АВСD за исключением 4 см, т.к. выделенный квадрат по периметру обложен прямоугольниками шириной 2 см. Получается, что с каждой стороны выделенного квадрата добавлено по 2 см.
Сторона выделенного квадрата 9-4 = 5 (см).
Периметр его равен 5*4 = 20 (см)
Ответ: Р закраш.ч. = 20 см.
3) Незакрашенная часть многоугольника АВСD представляет из себя четыре равных прямоугольника. АВСD - квадрат.
Ширина прямоугольника известна: 2 см (по рисунку).
Сторона АВСD равна 9 см. Она состоит из длины незакрашенного прямоугольника и его ширины. Ширину мы знаем - 2 см.
Длина незакрашенного прямоугольника 9 - 2 = 7 (см).
Площадь одного незакрашенного прямоугольника (длина умноженная на высоту):
7*2 = 14 (см²)
Таких прямоугольников четыре. Значит площадь незакрашенной части АВСD равнва 4*14 = 56 (см²)
Ответ: S незакраш.ч. = 56 см².