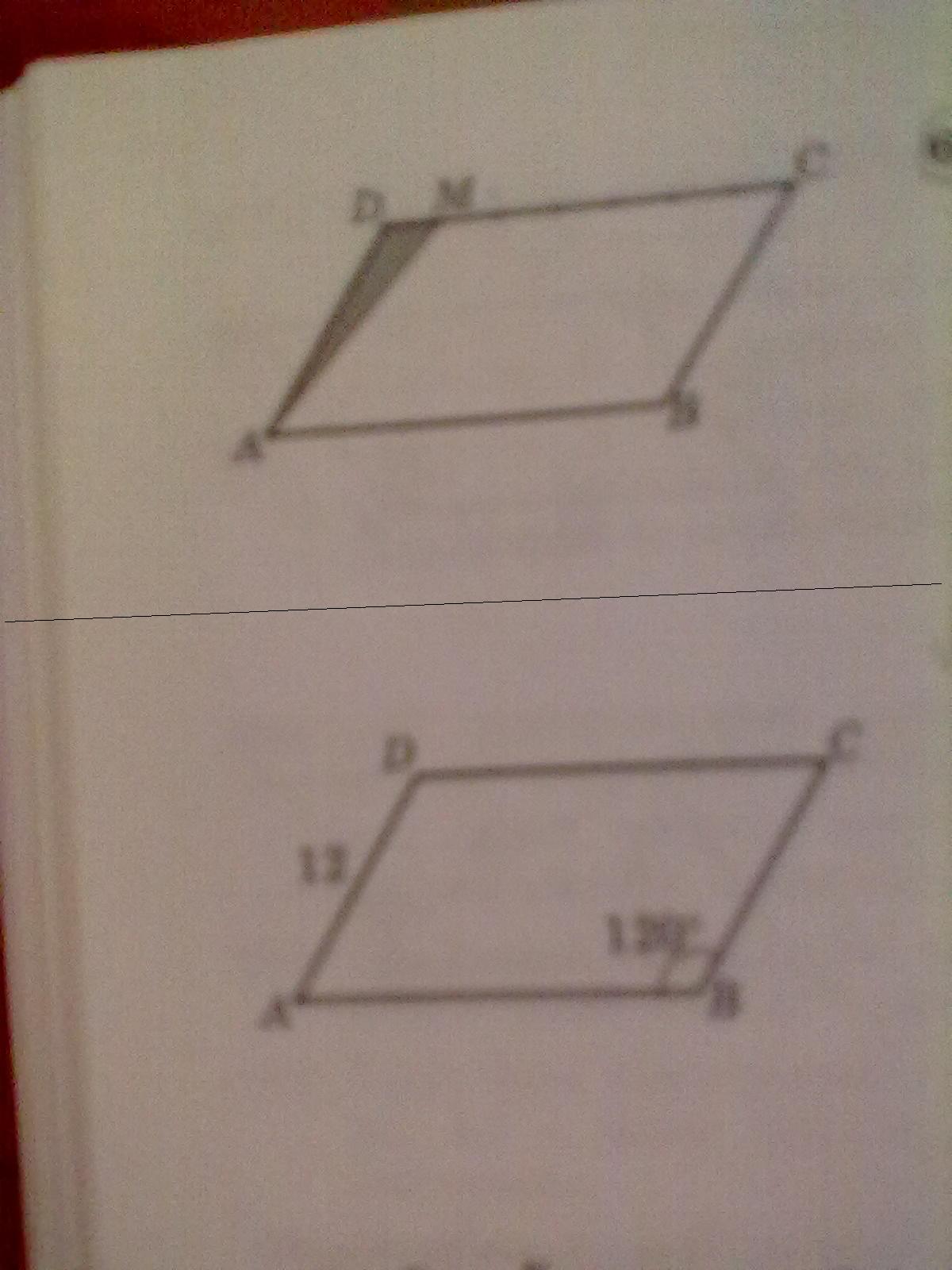
1)ABCD-параллеграмм
   DM-1/7
   S(ADM)=6см2
   S(BCD)-?

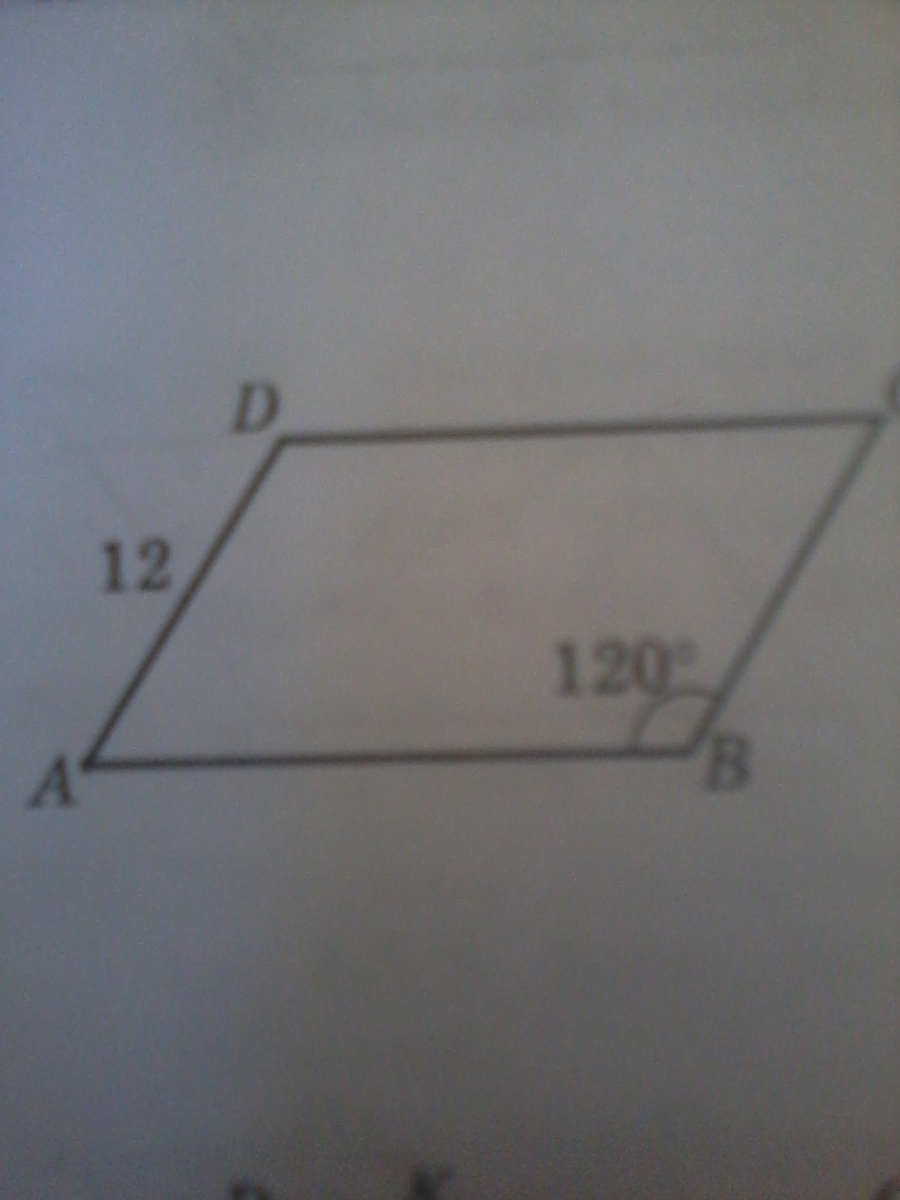
2)ABCD-параллелограмм
   AD-12
   DC=32/V3
   B=120 
   S(ABCD)-?

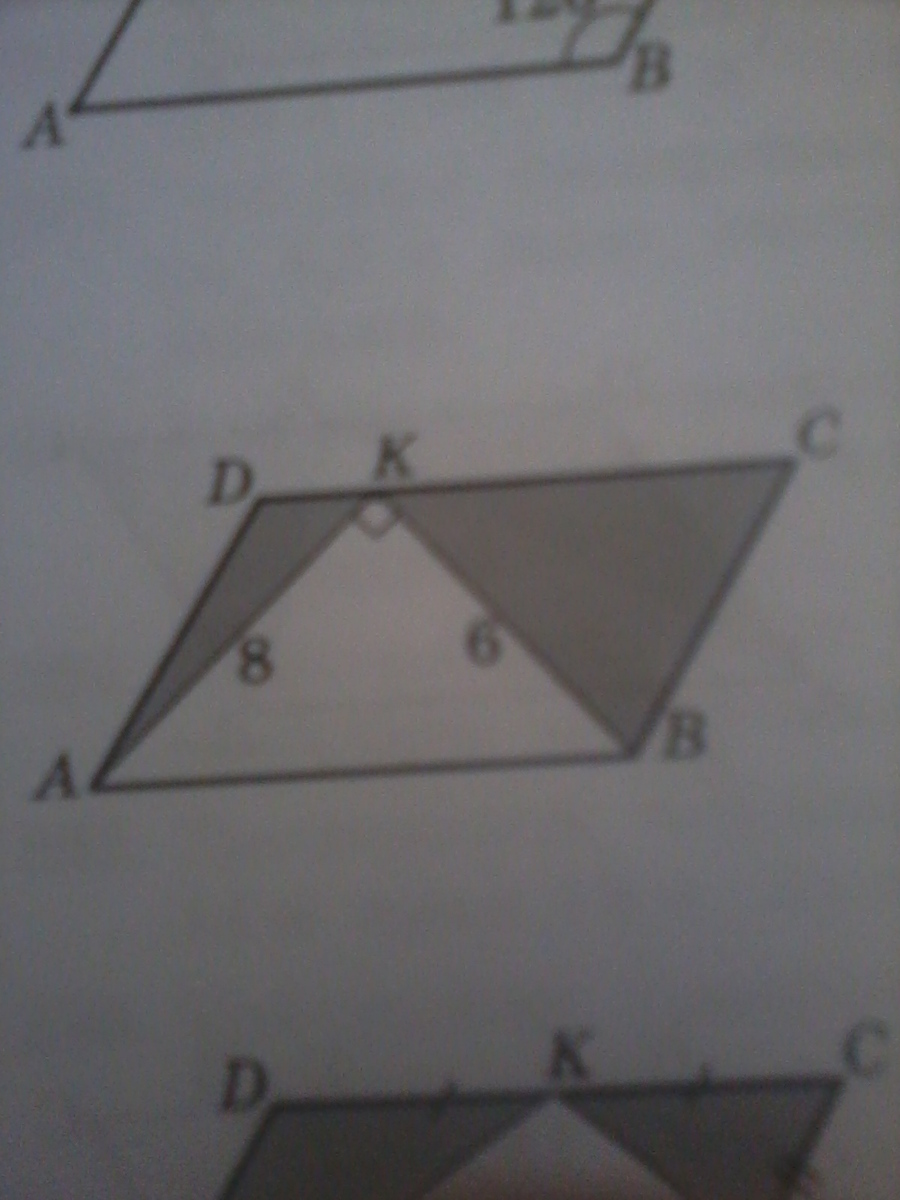
3)ABCD-параллелограмм
  AKM=90
   AK=8. BK=6
    S-?

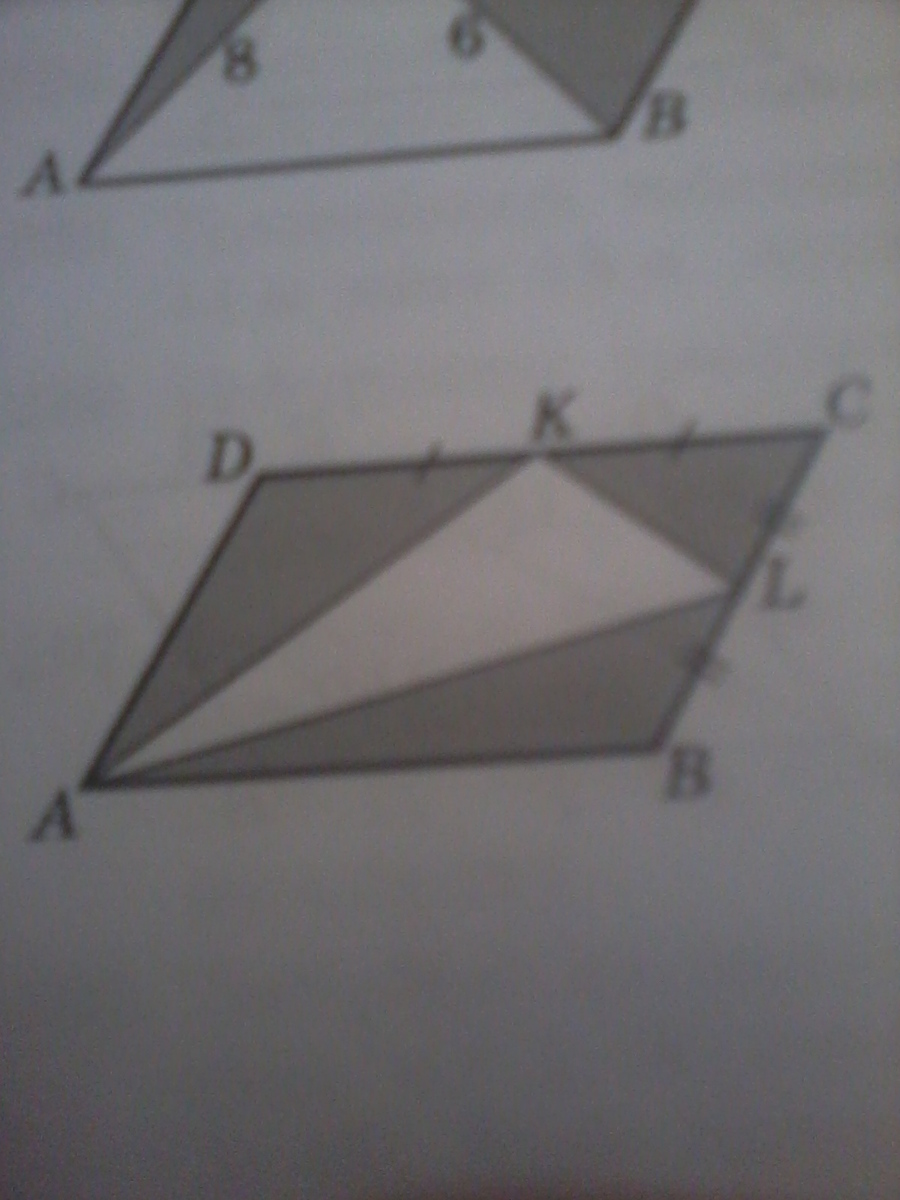
4)ABCD-параллелограмм
   S(ABCD)=24cm2
   S(AKL)-?

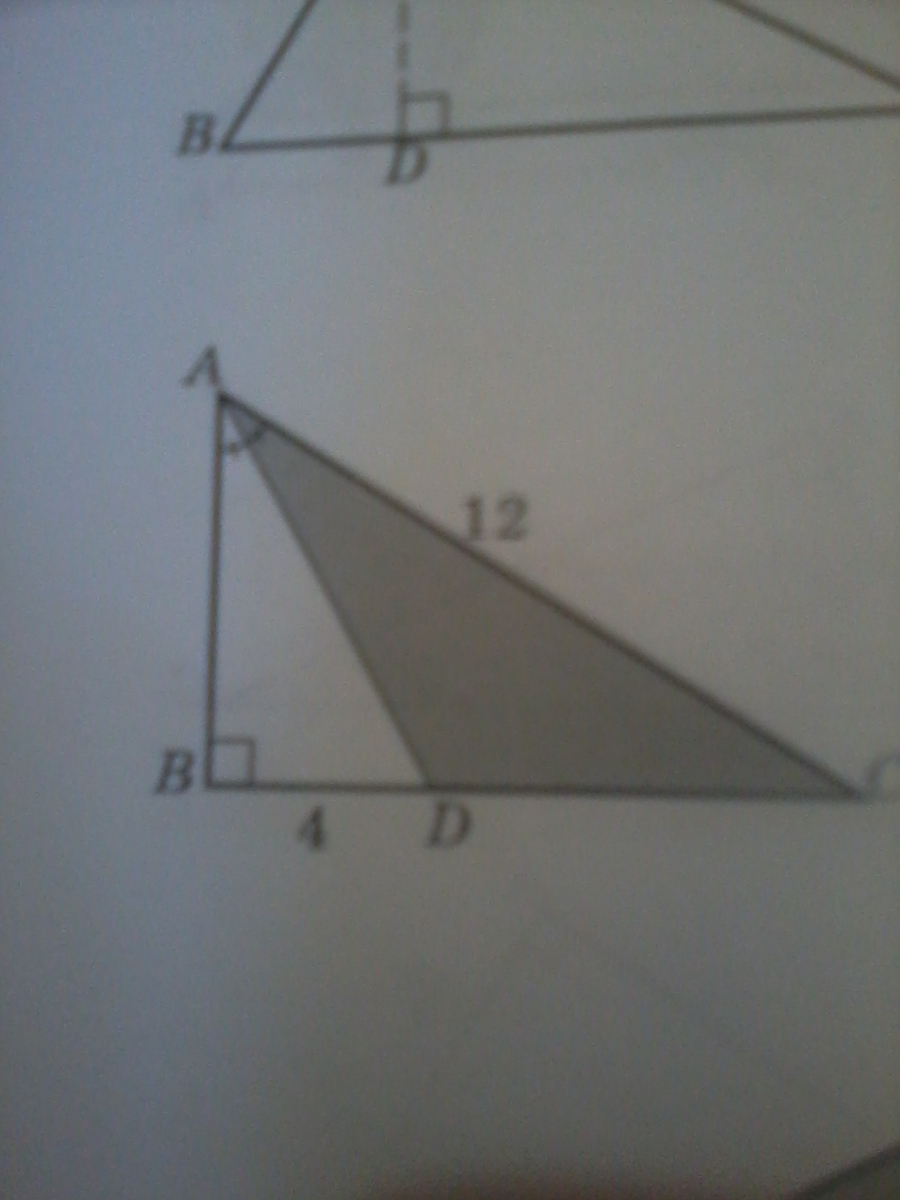
5)ABC-треугольник
    AD-биссектриса
     BD=4
     AC=12
    S(ADC)-?

1) если по условию DM = DC·1 / 7, то DM = x, DC= 7x, значит CD / DM = 7 / 1 = 7,

а треугольники ADM и АDC имеют общую высоту, значит их площади относятся как их основания: S1 / S2 = CD / DM ( где S1 - площадь ACD, S2 - площадь АМD )  ,

отсюда S1 =  7 * S2 = 7 * 6 = 42 .

2) угол D = угол В =120, находим площадь параллелограмма :

а * в * sin 120 =  а * в * sin ( 90 + 30 ) =  а * в * cos 30 =

= 12 * ( 32 / корень из 3 ) * ( корень из 3 / 2 ) = 192 .

5) Биссектриса делит противолежащую сторону на отрезки пропрциональные прилегающим сторонам, значит АВ / АС = ВD / DС ( АВ / 12 = 4 / DС ), следовательно

АВ * DС = 12 * 4. Площадь АDС=1 / 2 * АВ * DС = 1 / 2 (12 * 4) = 24.