Алгебра, вопрос задал Аноним , 6 лет назад

1.3 Выполните возведение в степень​

Приложения:

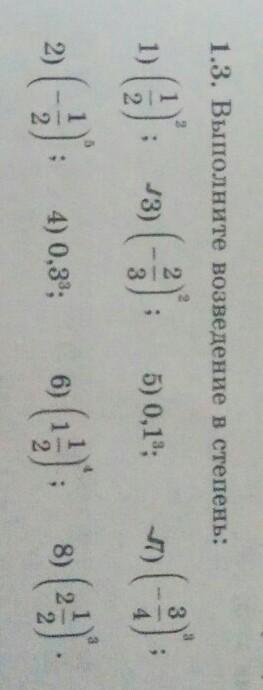
Ответы на вопрос

Ответил SirWallon
1

Объяснение:

1).

( \frac{1}{2})^{2} = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4}

2).

( - \frac{1}{2})^{5} = ( - \frac{1}{2}) \times ( - \frac{1}{2}) \times ( - \frac{1}{2}) \times ( - \frac{1}{2}) \times ( - \frac{1}{2}) = - \frac{1}{32}

3).

( - \frac{2}{3})^{2} = ( - \frac{2}{3}) \times ( - \frac{2}{3}) = \frac{4}{9}

4).

0.3 ^{3} = 0.3 \times 0.3 \times 0.3 = 0.027

5).

{0.1}^{3} = 0.1 \times 0.1 \times 0.1 = 0.001

6).

(1 \frac{1}{2}) ^{4} = (\frac{3}{2}) ^{4} = \frac{81}{16} = 5 \frac{1}{16}

7).

( - \frac{3}{4})^{3} = - \frac{27}{64}

8).

(2 \frac{1}{2})^{3} = ( \frac{5}{2})^{3} = \frac{125}{8} = 15 \frac{5}{8}

Ответил NNNLLL54
0

Ответ:

\Big(\dfrac{1}{2}\Big)^2=\dfrac{1}{4}\ \ ,\ \ \ \ \ \ \Big(-\dfrac{1}{2}\Big)^5=-\dfrac{1}{32}\ \ ,\ \ \ \ \ \ \Big(-\dfrac{2}{3}\Big)^2=\dfrac{4}{9}\ \ ,\\\\\\0,3^3=0,3\cdot 0,3\cdot 0,3=0,027\\\\\\0,1^3=0,1\cdot 0,1\cdot 0,1=0,001\\\\\Big(1\dfrac{1}{2}\Big)^4=\Big(\dfrac{3}{2}\Big)^4=\dfrac{3^4}{2^4}=\dfrac{81}{16}\\\\\\\Big(-\dfrac{3}{4}\Big)^3=-\dfrac{3^3}{4^3}=-\dfrac{27}{64}\\\\\\\Big(2\dfrac{1}{2}\Big)^3=\Big(\dfrac{5}{2}\Big)^3=\dfrac{5^3}{2^3}=\dfrac{125}{8}

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Математика, 1 год назад
вычисли 43м - 6м 8мм равно м дм см мм...
Русский язык, 1 год назад
сколько букв и звуков в слове орех,сцапать,деревья...
Математика, 6 лет назад
1. Известно, что значение произведения 254•337•234 равно одному из указанных ниже чисел. Найди это число, не используя Умножения: а. 23474213 б.20029932 в. 1348746 г. 2003454​...
История, 6 лет назад
3.Какие европейские государства в то время были ведущими колониальными державами? СРОЧНО​...
Математика, 8 лет назад
1 сутка.16 часов равно сколькочасов...
История, 8 лет назад
Вывод для таблицы "основные итоги развития общества в период раннего нового времени " КРАТКО!!!!