1.24. Точка движется в плоскости xoy по закону:
x =10t, y=9t(1-2t) . Найти уравнение траектории y= f (x) и изобразить ее
графически; вектор скорости V

и ускорения a

в зависимости от
времени; момент времени t0, в который вектор ускорения a

составляет
угол π/3 с вектором скорости V

. Ответ: y 0,9x(1 0,2x),t 0,41c 0    .

1)
Чтобы найти ТРАЕКТОРИЮ движения необходимо исключить время их уравнений движения:

x =10*t
y = 9*t -18*t²

Из первого уравнения:
t = x/10
Тогда:
y = 9*x/10 - 18*(x/10)²
y = 0,9*x - 0,18*x²
y = 0,9*x (1 - 0,2*x)

2)
Скорость вдоль ОХ
Vx = x' = 10 м/с
Ускорение равно нулю

Скорость вдоль ОY
Vy = y' = 9 - 36*t
Ускорение:
a = - 36 м/с²


(Дальше условие не понятно - изображены какие-то квадратики :(((

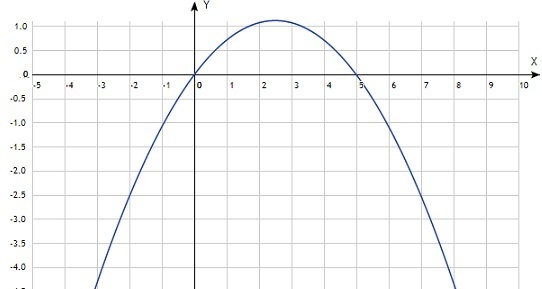
График функции в приложенном скрине

А время? .. полное условие . вектор скорости V ускорения a в зависимости от
времени; момент времени t0, в который вектор ускорения a составляет
угол π/3 с вектором скорости V. Ответ t0=0.41с

От времени у меня есть ответ: Vx(t) = 10 м/с - равномерное прямолинейное движение. Vy(t) = 9-36*t ; тогда V(t)= (10^2+(9-36*t)^2) ^(1/2) . a(t) = 36 (по модулю). С углом - не врубаюсь...