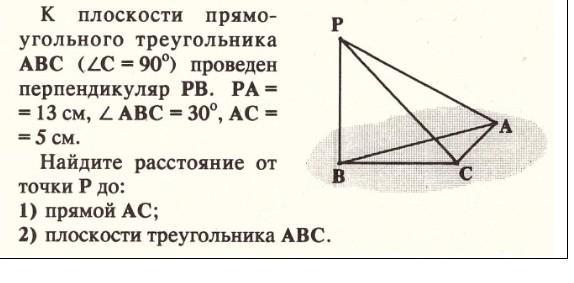
0 К плоскости прямо- угольного треугольника ABC_(ZC = 90º) проведен перпендикуляр PB. PA= = 13 см, Z ABC = 30º, AC = = 5 см. Найдите расстояние от точки Р до: P 1) прямой АС; 2) плоскости треугольника ABC.​

Ответ:

Расстояние от точки Р до прямой АС равно 12см

Расстояние от точки Р до плоскости треугольника равно √69см

Объяснение:

∆АВС - прямоугольный треугольник.

АС- катет против угла 30°

АВ=2*АС=2*5=10см

Теорема Пифагора:

ВС=√(АВ²-АС²)=√(10²-5²)=5√3см

∆РВА- прямоугольный треугольник.

Теорема Пифагора:

РВ=√(РА²-АВ²)=√(13²-10²)=

=√(169-100)=√69см расстояние от точки Р до плоскости треугольника ∆АВС;

∆РВС- прямоугольный треугольник.

Теорема Пифагора:

РС=√(РВ²+ВС²)=√((√69)²+(5√3)²)=

=√(69+75)=√144=12см расстояние от точки Р до прямой АС