..........................

Відповідь:
S(ABCD)=4,8см²

Розв'язання:
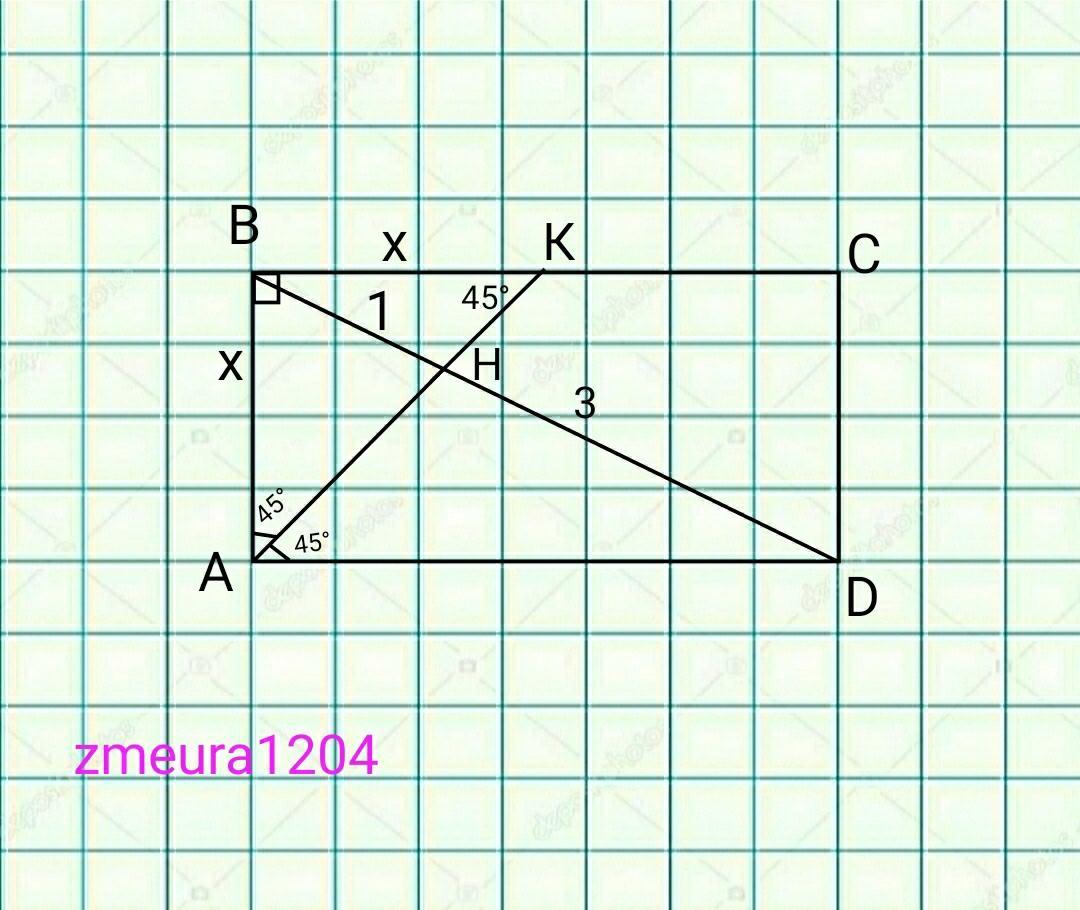
АН- бісектриса кута ∠А. Проведемо її до перехрестя з стороною ВС.
∆АВК- прямокутний, рівнобедрений трикутник.
Нехай ВК буде х, тоді АВ також буде х.
Розглянемо ∆ВНК і ∆АНD.
∠BKH=∠HAD, внутрішні навхрест при паралельних прямих ВС||АD, січною АК.
∠ВНК=∠АНD, вертикальні кути.
∆ВНК~∆АНD, за першою ознакою, за двома кутами.
k=ВН/НD=1/3.
BH/HD=BK/AD.
BK=x, тому АD=3x.
∆ABD- прямокутний трикутник.
За теоремою Піфагора
АВ²+АD²=BD²,
складаємо рівняння:
х²+(3х²)=4²
х²+9х²=16
10х²=16
х²=16/10
х=√(16/10)
х=4/√10 см сторона АВ.
3*4/√10=12/√10 см сторона АD.
S(ABCD)=AB*AD=4/√10*12/√10=
=48/10=4,8см²