Математика, вопрос задал kamilmatematik100504 , 6 лет назад

..................................

Приложения:

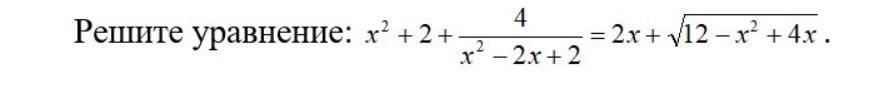
plus380972527679: х=2??

kamilmatematik100504: а решение ?

Ответы на вопрос

Ответил leprekon882

$x^2+2+\dfrac{4}{x^2-2x+2}=2x+\sqrt{12-x^2+4x}$

$(x-1)^2+1+\dfrac{4}{(x-1)^2+1}=\sqrt{16-(x-2)^2}$

Поскольку $(x-1)^2+1 > 0$ для любых x, то применимо неравенство Коши:

$(x-1)^2+1+\dfrac{4}{(x-1)^2+1}\geq2\sqrt{\Big((x-1)^2+1\Big)\cdot \dfrac{4}{(x-1)^2+1}}=4$

Правая часть уравнения $f(x)=\sqrt{16-(x-2)^2}\geq0$ на области определения. Наименьшее значение в точке $x=2$ равное $4$

Ответ: x = 2.

Предыдущий вопрос

Новые вопросы

Русский язык, 1 год назад

Русский язык, 1 год назад

Алгебра, 6 лет назад

Алгебра, 6 лет назад

Алгебра, 8 лет назад

Физика, 8 лет назад